第五章：图像分类

从本章开始学习深度学习机制，创建架构，从训练中获得最佳结果，加快速度和查看神经网络的内部情况，找到可能的问题并解决他们。

本章目标

我们将从重复第一章中查看的相同基本应用程序开始，但我们将做两件事：

让它们变得更好。
将它们应用于更多类型的数据。

从狗和猫识别到宠物品种识别

下载宠物数据

1 2	from fastai2.vision.all import * path = untar_data(URLs.PETS)

了解数据布局

现在，如果我们要理解如何从每个图像中提取每只宠物的品种，我们需要了解数据是如何布局的。数据布局的细节是深度学习难题的重要组成部分。数据通常以以下两种方式之一提供：

表示数据项的个别文件，例如文本文档或图像，可能组织成文件夹或具有表示有关这些项信息的文件名
数据表（例如，以 CSV 格式）中的数据，其中每行是一个项目，可能包括文件名，提供表中数据与其他格式（如文本文档和图像）中数据之间的连接

有一些例外情况——特别是在基因组学等领域，可能存在二进制数据库格式或甚至网络流——但总体而言，您将处理的绝大多数数据集将使用这两种格式的某种组合。

要查看数据集中的内容，我们可以使用ls方法：

path.ls()

1	(#3) [Path('annotations'),Path('images'),Path('models')]

与文档中结果不同的是现在下载的这个数据集内容如下：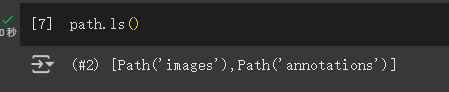

我们可以看到这个数据集为我们提供了images和annotations目录。数据集的网站告诉我们annotations目录包含有关宠物所在位置而不是它们是什么的信息。

查看images的内容：

1	(path/"images").ls()

(#7394) [Path('images/great_pyrenees_173.jpg'),Path('images/wheaten_terrier_46.j
 > pg'),Path('images/Ragdoll_262.jpg'),Path('images/german_shorthaired_3.jpg'),P
 > ath('images/american_bulldog_196.jpg'),Path('images/boxer_188.jpg'),Path('ima
 > ges/staffordshire_bull_terrier_173.jpg'),Path('images/basset_hound_71.jpg'),P
 > ath('images/staffordshire_bull_terrier_37.jpg'),Path('images/yorkshire_terrie
 > r_18.jpg')...]

在 fastai 中，大多数返回集合的函数和方法使用一个名为L的类。这个类可以被认为是普通 Python list类型的增强版本，具有用于常见操作的附加便利。例如，当我们在笔记本中显示这个类的对象时，它会以这里显示的格式显示。首先显示的是集合中的项目数，前面带有#。在前面的输出中，你还会看到列表后面有省略号。这意味着只显示了前几个项目，这是件好事，因为我们不希望屏幕上出现超过 7000 个文件名！

通过检查这些文件名，我们可以看到它们似乎是如何结构化的。每个文件名包含宠物品种，然后是一个下划线（_），一个数字，最后是文件扩展名。我们需要创建一段代码，从单个Path中提取品种。Jupyter 笔记本使这变得容易，因为我们可以逐渐构建出可用的东西，然后用于整个数据集。在这一点上，我们必须小心不要做太多假设。例如，如果你仔细观察，你可能会注意到一些宠物品种包含多个单词，因此我们不能简单地在找到的第一个_字符处中断。为了让我们能够测试我们的代码，让我们挑选出一个这样的文件名：

如何利用好文件名

正则表达式

从这样的字符串中提取信息的最强大和灵活的方法是使用regular expression，也称为regex。正则表达式是一种特殊的字符串，用正则表达式语言编写，它指定了一个一般规则，用于决定另一个字符串是否通过测试（即“匹配”正则表达式），并且可能用于从另一个字符串中提取特定部分。在这种情况下，我们需要一个正则表达式从文件名中提取宠物品种。

正则表达式示例：使用findall方法来对fname对象的文件名尝试一个正则表达式。

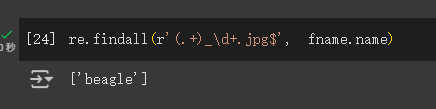
1	re.findall(r'(.+)_\d+.jpg$', fname.name)#这个正则表达式提取出所有字符，直到最后一个下划线字符，只要后续字符是数字，然后是 JPEG 文件扩展名。

1	['great_pyrenees']

利用RegexLabeller类标记整个数据集，使用了数据块 API，我们在第二章中看到过（实际上，我们几乎总是使用数据块 API——它比我们在第一章中看到的简单工厂方法更灵活）

pets = DataBlock(blocks = (ImageBlock, CategoryBlock),
                 get_items=get_image_files,
                 splitter=RandomSplitter(seed=42),
                 get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'),
                 item_tfms=Resize(460),
                 batch_tfms=aug_transforms(size=224, min_scale=0.75))
dls = pets.dataloaders(path/"images")

这个DataBlock调用中一个重要的部分是我们以前没有见过的这两行：

1 2	item_tfms=Resize(460), batch_tfms=aug_transforms(size=224, min_scale=0.75)

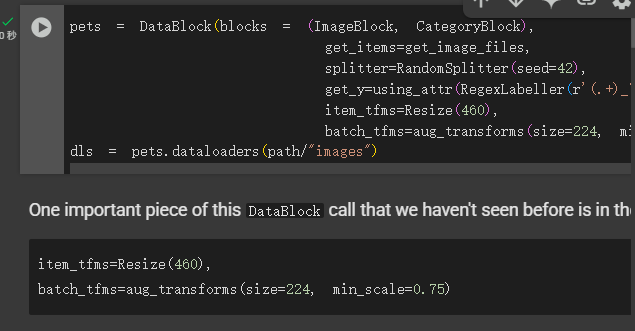
这些行实现了一个我们称之为预调整的 fastai 数据增强策略。预调整是一种特殊的图像增强方法，旨在最大限度地减少数据破坏，同时保持良好的性能。

预调整

目的：

我们需要的图像具有相同的尺寸，这样它们可以整合成张量传递给 GPU。
我们还希望最小化我们执行的不同增强计算的数量。性能要求表明，我们应该尽可能将我们的增强变换组合成更少的变换（以减少计算数量和损失操作的数量）。

预调整策略：

将图像调整为相对“大”的尺寸，即明显大于目标训练尺寸。
将所有常见的增强操作（包括调整大小到最终目标大小）组合成一个，并在 GPU 上一次性执行组合操作，而不是单独执行操作并多次插值。

步骤

调整大小，创建足够大的图像，使其内部区域有多余的边距，以允许进一步的增强变换而不会产生空白区域
这个转换通过调整大小为一个正方形，使用一个大的裁剪尺寸来实现。在训练集上，裁剪区域是随机选择的，裁剪的大小被选择为覆盖图像宽度或高度中较小的那个。
GPU 用于所有数据增强，并且所有潜在破坏性操作都一起完成，最后进行单次插值。

这张图片展示了两个步骤：

裁剪全宽或全高：这在item_tfms中，因此它应用于每个单独的图像，然后再复制到 GPU。它用于确保所有图像具有相同的尺寸。在训练集上，裁剪区域是随机选择的。在验证集上，总是选择图像的中心正方形。
随机裁剪和增强：这在batch_tfms中，因此它一次在 GPU 上应用于整个批次，这意味着速度快。在验证集上，只有调整大小到模型所需的最终大小。在训练集上，首先进行随机裁剪和任何其他增强。

要在 fastai 中实现此过程，您可以使用Resize作为具有大尺寸的项目转换，以及RandomResizedCrop作为具有较小尺寸的批处理转换。如果在aug_transforms函数中包含min_scale参数，RandomResizedCrop将为您添加，就像在上一节中的DataBlock调用中所做的那样。或者，您可以在初始Resize中使用pad或squish而不是crop（默认值）。

图 5-2 显示了一个图像经过缩放、插值、旋转，然后再次插值（这是所有其他深度学习库使用的方法），显示在右侧，以及一个图像经过缩放和旋转作为一个操作，然后插值一次（fastai 方法），显示在左侧。

图 5-2。fastai 数据增强策略（左）与传统方法（右）的比较

您可以看到右侧的图像定义不够清晰，在左下角有反射填充伪影；此外，左上角的草完全消失了。我们发现，在实践中，使用预调整显著提高了模型的准确性，通常也会加快速度。

fastai 库还提供了简单的方法来检查您的数据在训练模型之前的外观，这是一个非常重要的步骤。我们将在下一步中看到这些。

检查和调试 DataBlock

我们永远不能假设我们的代码完美运行。编写DataBlock就像编写蓝图一样。如果您的代码中有语法错误，您将收到错误消息，但是您无法保证您的模板会按照您的意图在数据源上运行。因此，在训练模型之前，您应该始终检查您的数据。

您可以使用show_batch方法来执行此操作：

1	dls.show_batch(nrows=1, ncols=3)

检查一下数据吧，确保图像中的狗和标注的品种相对应。（制作数据集的大概率可能会犯一些小错误，哪怕你也是所以检查一下总没错的）。

如果在构建DataBlock时出现错误，您可能在此步骤之前不会看到它。为了调试这个问题，我们鼓励您使用summary方法。它将尝试从您提供的源创建一个批次，并提供大量细节。此外，如果失败，您将准确地看到错误发生的位置，并且库将尝试为您提供一些帮助。例如，一个常见的错误是忘记使用Resize转换，因此最终得到不同大小的图片并且无法将它们整理成批次。在这种情况下，摘要将如下所示（请注意，自撰写时可能已更改确切文本，但它将给您一个概念）：

pets1 = DataBlock(blocks = (ImageBlock, CategoryBlock),
                 get_items=get_image_files,
                 splitter=RandomSplitter(seed=42),
                 get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'))
pets1.summary(path/"images")

Setting-up type transforms pipelines
Collecting items from /home/sgugger/.fastai/data/oxford-iiit-pet/images
Found 7390 items
2 datasets of sizes 5912,1478
Setting up Pipeline: PILBase.create
Setting up Pipeline: partial -> Categorize

Building one sample
  Pipeline: PILBase.create
    starting from
      /home/sgugger/.fastai/data/oxford-iiit-pet/images/american_bulldog_83.jpg
    applying PILBase.create gives
      PILImage mode=RGB size=375x500
  Pipeline: partial -> Categorize
    starting from
      /home/sgugger/.fastai/data/oxford-iiit-pet/images/american_bulldog_83.jpg
    applying partial gives
      american_bulldog
    applying Categorize gives
      TensorCategory(12)

Final sample: (PILImage mode=RGB size=375x500, TensorCategory(12))

Setting up after_item: Pipeline: ToTensor
Setting up before_batch: Pipeline:
Setting up after_batch: Pipeline: IntToFloatTensor

Building one batch
Applying item_tfms to the first sample:
  Pipeline: ToTensor
    starting from
      (PILImage mode=RGB size=375x500, TensorCategory(12))
    applying ToTensor gives
      (TensorImage of size 3x500x375, TensorCategory(12))

Adding the next 3 samples

No before_batch transform to apply

Collating items in a batch
Error! It's not possible to collate your items in a batch
Could not collate the 0-th members of your tuples because got the following
shapes:
torch.Size([3, 500, 375]),torch.Size([3, 375, 500]),torch.Size([3, 333, 500]),
torch.Size([3, 375, 500])

您可以看到我们如何收集数据并拆分数据，如何从文件名转换为样本（元组（图像，类别）），然后应用了哪些项目转换以及如何在批处理中无法整理这些样本（因为形状不同）。

一旦您认为数据看起来正确，我们通常建议下一步应该使用它来训练一个简单的模型。我们经常看到人们将实际模型的训练推迟得太久。结果，他们不知道他们的基准结果是什么样的。也许您的问题不需要大量花哨的领域特定工程。或者数据似乎根本无法训练模型。这些都是您希望尽快了解的事情。

对于这个初始测试，我们将使用与第一章中使用的相同简单模型：

1 2	learn = cnn_learner(dls, resnet34, metrics=error_rate) learn.fine_tune(2)

epoch	train_loss	valid_loss	error_rate	time
0	1.491732	0.337355	0.108254	00:18
epoch	train_loss	valid_loss	error_rate	time
—-	—-	—-	—-	—-
0	0.503154	0.293404	0.096076	00:23
1	0.314759	0.225316	0.066306	00:23

正如我们之前简要讨论过的，当我们拟合模型时显示的表格展示了每个训练周期后的结果。记住，一个周期是对数据中所有图像的完整遍历。显示的列是训练集中项目的平均损失、验证集上的损失，以及我们请求的任何指标——在这种情况下是错误率。

请记住损失是我们决定用来优化模型参数的任何函数。但是我们实际上并没有告诉 fastai 我们想要使用什么损失函数。那么它在做什么呢？fastai 通常会根据您使用的数据和模型类型尝试选择适当的损失函数。在这种情况下，我们有图像数据和分类结果，所以 fastai 会默认使用交叉熵损失。

交叉熵损失

交叉熵损失是一个类似于我们在上一章中使用的损失函数，但是（正如我们将看到的）有两个好处：

即使我们的因变量有两个以上的类别，它也能正常工作。
这将导致更快速、更可靠的训练。

要理解交叉熵损失如何处理具有两个以上类别的因变量，我们首先必须了解损失函数看到的实际数据和激活是什么样子的。

查看激活和标签

让我们看看我们模型的激活。要从我们的DataLoaders中获取一批真实数据，我们可以使用one_batch方法：

1	x,y = dls.one_batch()

正如您所见，这返回了因变量和自变量，作为一个小批量。让我们看看我们的因变量中包含什么：

TensorCategory([11,  0,  0,  5, 20,  4, 22, 31, 23, 10, 20,  2,  3, 27, 18, 23,
 > 33,  5, 24,  7,  6, 12,  9, 11, 35, 14, 10, 15,  3,  3, 21,  5, 19, 14, 12,
 > 15, 27,  1, 17, 10,  7,  6, 15, 23, 36,  1, 35,  6,
         4, 29, 24, 32,  2, 14, 26, 25, 21,  0, 29, 31, 18,  7,  7, 17],
 > device='cuda:5')

实际预测是 37 个介于 0 和 1 之间的概率，总和为 1：

1	len(preds[0]),preds[0].sum()

1	(37, tensor(1.0000))

为了将我们模型的激活转换为这样的预测，我们使用了一个叫做softmax的激活函数

Softmax

在我们的分类模型中，我们在最后一层使用 softmax 激活函数，以确保激活值都在 0 到 1 之间，并且它们总和为 1。

Softmax 类似于我们之前看到的 sigmoid 函数。作为提醒，sigmoid 看起来像这样：

1	plot_function(torch.sigmoid, min=-4,max=4)

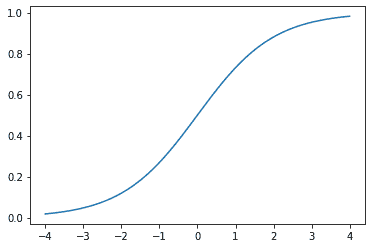
我们可以将这个函数应用于神经网络的一个激活列，并得到一个介于 0 和 1 之间的数字列，因此对于我们的最后一层来说，这是一个非常有用的激活函数。

现在想象一下，如果我们希望目标中有更多类别（比如我们的 37 种宠物品种）。这意味着我们需要比单个列更多的激活：我们需要一个激活每个类别。例如，我们可以创建一个预测 3 和 7 的神经网络，返回两个激活，每个类别一个——这将是创建更一般方法的一个很好的第一步。让我们只是使用一些标准差为 2 的随机数（因此我们将randn乘以 2）作为示例，假设我们有六个图像和两个可能的类别（其中第一列代表 3，第二列代表 7）：

1 2	acts = torch.randn((6,2))*2 acts

tensor([[ 0.6734,  0.2576],
        [ 0.4689,  0.4607],
        [-2.2457, -0.3727],
        [ 4.4164, -1.2760],
        [ 0.9233,  0.5347],
        [ 1.0698,  1.6187]])

我们不能直接对这个进行 sigmoid 运算，因为我们得不到行相加为 1 的结果（我们希望 3 的概率加上 7 的概率等于 1）：

1	acts.sigmoid()

tensor([[0.6623, 0.5641],
        [0.6151, 0.6132],
        [0.0957, 0.4079],
        [0.9881, 0.2182],
        [0.7157, 0.6306],
        [0.7446, 0.8346]])

在第四章中，我们的神经网络为每个图像创建了一个单一激活，然后通过sigmoid函数传递。这个单一激活代表了模型对输入是 3 的置信度。二进制问题是分类问题的一种特殊情况，因为目标可以被视为单个布尔值，就像我们在mnist_loss中所做的那样。但是二进制问题也可以在任意数量的类别的分类器的更一般上下文中考虑：在这种情况下，我们碰巧有两个类别。正如我们在熊分类器中看到的，我们的神经网络将为每个类别返回一个激活。

那么在二进制情况下，这些激活实际上表示什么？一对激活仅仅表示输入是 3 还是 7 的相对置信度。总体值，无论它们是高还是低，都不重要，重要的是哪个更高，以及高多少。

我们期望，由于这只是表示相同问题的另一种方式，我们应该能够直接在我们的神经网络的两个激活版本上使用sigmoid。事实上我们可以！我们只需取神经网络激活之间的差异，因为这反映了我们对输入是 3 还是 7 更有把握的程度，然后取其 sigmoid：

1	(acts[:,0]-acts[:,1]).sigmoid()

1	tensor([0.6025, 0.5021, 0.1332, 0.9966, 0.5959, 0.3661])

第二列（它是 7 的概率）将是该值从 1 中减去的值。现在，我们需要一种适用于多于两列的方法。事实证明，这个名为softmax的函数正是这样的：

1	def softmax(x): return exp(x) / exp(x).sum(dim=1, keepdim=True)

术语：指数函数（exp）

定义为e**x，其中e是一个特殊的数字，约等于 2.718。它是自然对数函数的倒数。请注意，exp始终为正，并且增长非常迅速！

让我们检查softmax是否为第一列返回与sigmoid相同的值，以及这些值从 1 中减去的值为第二列：

1 2	sm_acts = torch.softmax(acts, dim=1) sm_acts

tensor([[0.6025, 0.3975],
        [0.5021, 0.4979],
        [0.1332, 0.8668],
        [0.9966, 0.0034],
        [0.5959, 0.4041],
        [0.3661, 0.6339]])

softmax是sigmoid的多类别等价物——每当我们有超过两个类别且类别的概率必须加起来为 1 时，我们必须使用它，即使只有两个类别，我们通常也会使用它，只是为了使事情更加一致。我们可以创建其他具有所有激活在 0 和 1 之间且总和为 1 的属性的函数；然而，没有其他函数与我们已经看到是平滑且对称的 sigmoid 函数具有相同的关系。此外，我们很快将看到 softmax 函数与我们将在下一节中看到的损失函数密切配合。

如果我们有三个输出激活，就像在我们的熊分类器中一样，为单个熊图像计算 softmax 看起来会像图 5-3 那样。

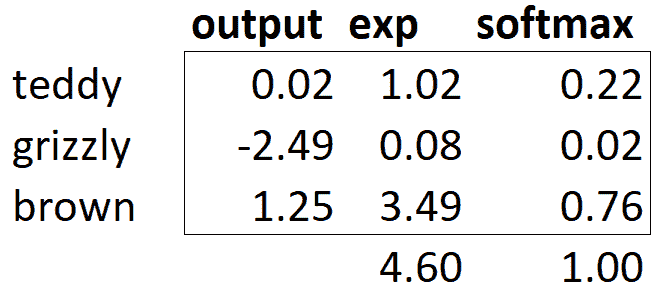
图 5-3. 熊分类器上 softmax 的示例

实际上，这个函数是做什么的呢？取指数确保我们所有的数字都是正数，然后除以总和确保我们将得到一堆加起来等于 1 的数字。指数还有一个很好的特性：如果我们激活中的某个数字略大于其他数字，指数将放大这个差异（因为它呈指数增长），这意味着在 softmax 中，该数字将更接近 1。

直观地，softmax 函数真的想要在其他类别中选择一个类别，因此在我们知道每张图片都有一个明确标签时，训练分类器时是理想的选择。（请注意，在推断过程中可能不太理想，因为有时您可能希望模型告诉您它在训练过程中看到的类别中没有识别出任何一个，并且不选择一个类别，因为它的激活分数略高。在这种情况下，最好使用多个二进制输出列来训练模型，每个列使用 sigmoid 激活。）

Softmax 是交叉熵损失的第一部分，第二部分是对数似然。

对数似然

在上一章中为我们的 MNIST 示例计算损失时，我们使用了这个：

1
2
3

def mnist_loss(inputs, targets):
    inputs = inputs.sigmoid()
    return torch.where(targets==1, 1-inputs, inputs).mean()

就像我们从 sigmoid 到 softmax 的转变一样，我们需要扩展损失函数，使其能够处理不仅仅是二元分类，还需要能够对任意数量的类别进行分类（在本例中，我们有 37 个类别）。我们的激活，在 softmax 之后，介于 0 和 1 之间，并且对于预测批次中的每一行，总和为 1。我们的目标是介于 0 和 36 之间的整数。

在二元情况下，我们使用torch.where在inputs和1-inputs之间进行选择。当我们将二元分类作为具有两个类别的一般分类问题处理时，它变得更容易，因为（正如我们在前一节中看到的）现在有两列包含等同于inputs和1-inputs的内容。因此，我们只需要从适当的列中进行选择。让我们尝试在 PyTorch 中实现这一点。对于我们合成的 3 和 7 的示例，假设这些是我们的标签：

1	targ = tensor([0,1,0,1,1,0])

这些是 softmax 激活：

sm_acts

tensor([[0.6025, 0.3975],
        [0.5021, 0.4979],
        [0.1332, 0.8668],
        [0.9966, 0.0034],
        [0.5959, 0.4041],
        [0.3661, 0.6339]])

然后对于每个targ项，我们可以使用它来使用张量索引选择sm_acts的适当列，如下所示：

1 2	idx = range(6) sm_acts[idx, targ]

1	tensor([0.6025, 0.4979, 0.1332, 0.0034, 0.4041, 0.3661])

为了准确了解这里发生了什么，让我们将所有列放在一起放在一个表中。这里，前两列是我们的激活，然后是目标，行索引，最后是前面代码中显示的结果：

3	7	targ	idx	loss
0.602469	0.397531	0	0	0.602469
0.502065	0.497935	1	1	0.497935
0.133188	0.866811	0	2	0.133188
0.99664	0.00336017	1	3	0.00336017
0.595949	0.404051	1	4	0.404051
0.366118	0.633882	0	5	0.366118

从这个表中可以看出，最后一列可以通过将targ和idx列作为索引，指向包含3和7列的两列矩阵来计算。这就是sm_acts[idx, targ]的作用。

这里真正有趣的是，这种方法同样适用于超过两列的情况。想象一下，如果我们为每个数字（0 到 9）添加一个激活列，然后targ包含从 0 到 9 的数字。只要激活列总和为 1（如果我们使用 softmax，它们将是这样），我们将有一个损失函数，显示我们预测每个数字的准确程度。

我们只从包含正确标签的列中选择损失。我们不需要考虑其他列，因为根据 softmax 的定义，它们加起来等于 1 减去与正确标签对应的激活。因此，使正确标签的激活尽可能高必须意味着我们也在降低其余列的激活。

PyTorch 提供了一个与sm_acts[range(n), targ]完全相同的函数（除了它取负数，因为之后应用对数时，我们将得到负数），称为nll_loss（NLL代表负对数似然）：

1	-sm_acts[idx, targ]

1	tensor([-0.6025, -0.4979, -0.1332, -0.0034, -0.4041, -0.3661])

1	F.nll_loss(sm_acts, targ, reduction='none')

1	tensor([-0.6025, -0.4979, -0.1332, -0.0034, -0.4041, -0.3661])

尽管它的名字是这样的，但这个 PyTorch 函数并不取对数。我们将在下一节看到原因，但首先，让我们看看为什么取对数会有用。

取对数

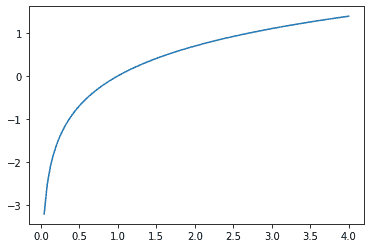
在前一节中我们看到的函数作为损失函数效果很好，但我们可以让它更好一些。问题在于我们使用的是概率，概率不能小于 0 或大于 1。这意味着我们的模型不会在乎它是预测 0.99 还是 0.999。确实，这些数字非常接近，但从另一个角度来看，0.999 比 0.99 自信程度高 10 倍。因此，我们希望将我们的数字从 0 到 1 转换为从负无穷到无穷。有一个数学函数可以做到这一点：对数（可用torch.log）。它对小于 0 的数字没有定义，并且如下所示：

1	plot_function(torch.log, min=0,max=4)

“对数”这个词让你想起了什么吗？对数函数有这个恒等式：

1 2	y = b**a a = log(y,b)

在这种情况下，我们假设log(y,b)返回log y 以 b 为底。然而，PyTorch 并没有这样定义log：Python 中的log使用特殊数字e（2.718…）作为底。

也许对数是您在过去 20 年中没有考虑过的东西。但对于深度学习中的许多事情来说，对数是一个非常关键的数学概念，所以现在是一个很好的时机来刷新您的记忆。关于对数的关键事情是这样的关系：

1	log(a*b) = log(a)+log(b)

当我们以这种格式看到它时，它看起来有点无聊；但想想这实际上意味着什么。这意味着当基础信号呈指数或乘法增长时，对数会线性增加。例如，在地震严重程度的里氏震级和噪音级别的分贝尺中使用。它也经常用于金融图表中，我们希望更清楚地显示复合增长率。计算机科学家喜欢使用对数，因为这意味着可以用加法代替修改，这样可以避免产生计算机难以处理的难以处理的规模。

TIP

对我们的概率取正对数或负对数的平均值（取决于是否是正确或不正确的类）给出了负对数似然损失。在 PyTorch 中，nll_loss假设您已经对 softmax 取了对数，因此不会为您执行对数运算。

请注意一下函数名称

nll_loss中的“nll”代表“负对数似然”，但实际上它根本不进行对数运算！它假设您已经已经进行了对数运算。PyTorch 有一个名为log_softmax的函数，以快速准确的方式结合了log和softmax。nll_loss设计用于在log_softmax之后使用。

当我们首先进行 softmax，然后对其进行对数似然，这种组合被称为交叉熵损失。在 PyTorch 中，这可以通过nn.CrossEntropyLoss来实现（实际上执行log_softmax然后nll_loss）：

1	loss_func = nn.CrossEntropyLoss()

正如您所看到的，这是一个类。实例化它会给您一个像函数一样行为的对象：

1	loss_func(acts, targ)

1	tensor(1.8045)

所有 PyTorch 损失函数都以两种形式提供，刚刚显示的类形式以及在F命名空间中提供的普通函数形式：

1	F.cross_entropy(acts, targ)

1	tensor(1.8045)

两者都可以正常工作，并且可以在任何情况下使用。我们注意到大多数人倾向于使用类版本，并且在 PyTorch 的官方文档和示例中更常见，因此我们也会倾向于使用它。

默认情况下，PyTorch 损失函数取所有项目的损失的平均值。您可以使用reduction='none'来禁用这一点：

1	nn.CrossEntropyLoss(reduction='none')(acts, targ)

1	tensor([0.5067, 0.6973, 2.0160, 5.6958, 0.9062, 1.0048])

模型解释

直接解释损失函数非常困难，因为它们被设计为计算机可以区分和优化的东西，而不是人类可以理解的东西。这就是为什么我们有指标。这些指标不用于优化过程，而只是帮助我们这些可怜的人类理解发生了什么。在这种情况下，我们的准确率已经看起来相当不错！那么我们在哪里犯了错误呢？

我们在第一章中看到，我们可以使用混淆矩阵来查看模型表现好和表现不佳的地方：

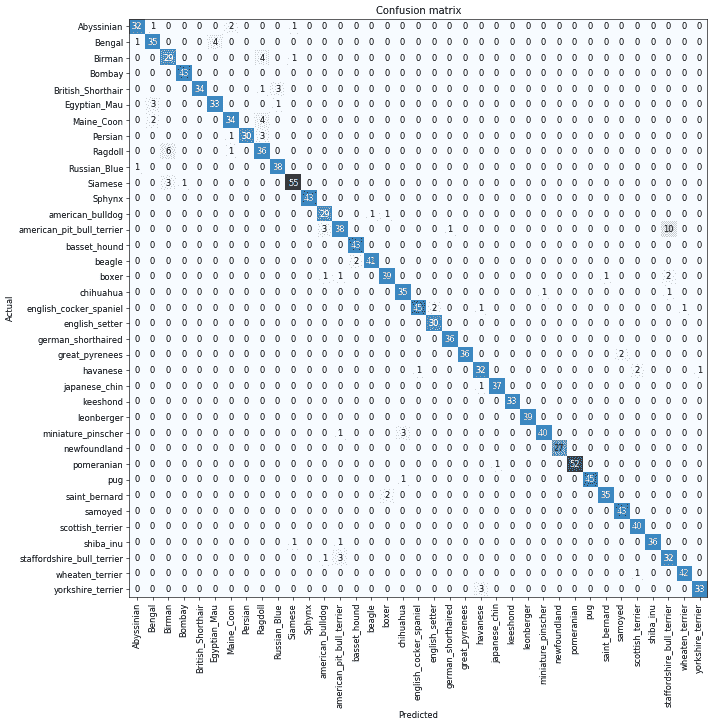
1 2	interp = ClassificationInterpretation.from_learner(learn) interp.plot_confusion_matrix(figsize=(12,12), dpi=60)

哦，亲爱的——在这种情况下，混淆矩阵很难阅读。我们有 37 种宠物品种，这意味着在这个巨大矩阵中有 37×37 个条目！相反，我们可以使用most_confused方法，它只显示混淆矩阵中预测错误最多的单元格（这里至少有 5 个或更多）：

1	interp.most_confused(min_val=5)

1 2	[('american_pit_bull_terrier', 'staffordshire_bull_terrier', 10), ('Ragdoll', 'Birman', 6)]

由于我们不是宠物品种专家，很难知道这些类别错误是否反映了识别品种时的实际困难。因此，我们再次求助于谷歌。一点点搜索告诉我们，这里显示的最常见的类别错误是即使是专家育种者有时也会对其存在分歧的品种差异。因此，这让我们有些安慰，我们正在走在正确的道路上。

我们似乎有一个良好的基线。现在我们可以做些什么来使它变得更好呢？

改进模型

解释迁移学习以及如何尽可能最好地微调我们的预训练模型，而不破坏预训练权重。

重点在于设置学习率（在fastai中有一个高效快捷的工具）

学习率查找器

学习率过高现象：

1 2	learn = cnn_learner(dls, resnet34, metrics=error_rate) learn.fine_tune(1, base_lr=0.1)

epoch	train_loss	valid_loss	error_rate	time
0	8.946717	47.954632	0.893775	00:20
epoch	train_loss	valid_loss	error_rate	time
—-	—-	—-	—-	—-
0	7.231843	4.119265	0.954668	00:24

现在问题来了怎么找到合适的学习率？

快使用学习率查找器。他的想法是从一个非常非常小的学习率开始，一个我们永远不会认为它太大而无法处理的学习率。我们用这个学习率进行一个 mini-batch，找到之后的损失，然后按一定百分比增加学习率（例如每次加倍）。然后我们再做另一个 mini-batch，跟踪损失，并再次加倍学习率。我们一直这样做，直到损失变得更糟没有变得更好。然后我们按照要求选择一个比这个点稍低的学习率：

比最小损失达到的地方少一个数量级（即最小值除以 10）
最后一次损失明显减少的点

学习率查找器计算曲线上的这些点来帮助您。这两个规则通常给出大致相同的值。在第一章中，我们没有指定学习率，而是使用了 fastai 库的默认值（即 1e-3）

关于mini-batch：我们已知在梯度下降中需要对所有样本进行处理过后然后走一步，那么如果我们的样本规模的特别大的话效率就会比较低。假如有500万，甚至5000万个样本(在我们的业务场景中，一般有几千万行，有些大数据有10亿行)的话走一轮迭代就会非常的耗时。这个时候的梯度下降叫做full batch。所以为了提高效率，我们可以把样本分成等量的子集。例如我们把100万样本分成1000份，每份1000个样本，这些子集就称为mini batch。然后我们分别用一个for循环遍历这1000个子集。针对每一个子集做一次梯度下降。然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。我们将遍历一次所有样本的行为叫做一个 epoch，也就是一个世代。在mini batch下的梯度下降中做的事情其实跟full batch一样，只不过我们训练的数据不再是所有的样本，而是一个个的子集。这样在mini batch我们在一个epoch中就能进行1000次的梯度下降，而在full batch中只有一次。这样就大大的提高了我们算法的运行速度。

1 2	learn = cnn_learner(dls, resnet34, metrics=error_rate) lr_min,lr_steep = learn.lr_find()

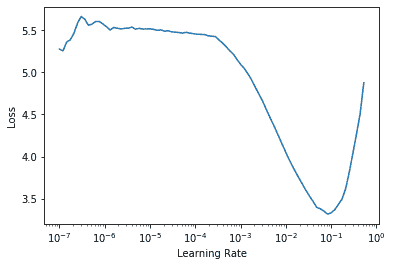
1	print(f"Minimum/10: {lr_min:.2e}, steepest point: {lr_steep:.2e}")

1	Minimum/10: 8.32e-03, steepest point: 6.31e-03

我们可以看到在 1e-6 到 1e-3 的范围内，没有什么特别的事情发生，模型不会训练。然后损失开始减少，直到达到最小值，然后再次增加。我们不希望学习率大于 1e-1，因为这会导致训练发散（您可以自行尝试），但 1e-1 已经太高了：在这个阶段，我们已经离开了损失稳定下降的阶段。

在这个学习率图中，看起来学习率约为 3e-3 可能是合适的，所以让我们选择这个：

1 2	learn = cnn_learner(dls, resnet34, metrics=error_rate) learn.fine_tune(2, base_lr=3e-3)

epoch	train_loss	valid_loss	error_rate	time
0	1.071820	0.427476	0.133965	00:19
epoch	train_loss	valid_loss	error_rate	time
—-	—-	—-	—-	—-
0	0.738273	0.541828	0.150880	00:24
1	0.401544	0.266623	0.081867	00:24

问卷调查

为什么我们首先在 CPU 上调整大小到较大尺寸，然后在 GPU 上调整到较小尺寸？

先在CPU上放大以高效处理大尺寸插值，再在GPU上缩小以利用并行加速动态增强并节省显存。

如果您不熟悉正则表达式，请查找正则表达式教程和一些问题集，并完成它们。查看书籍网站以获取建议。

一个可以将文件名字利用起来的程序

对于大多数深度学习数据集，数据通常以哪两种方式提供？

表示数据项的个别文件，例如文本文档或图像，可能组织成文件夹或具有表示有关这些项信息的文件名
数据表（例如，以 CSV 格式）中的数据，其中每行是一个项目，可能包括文件名，提供表中数据与其他格式（如文本文档和图像）中数据之间的连接

查阅L的文档，并尝试使用它添加的一些新方法。查阅 Python pathlib模块的文档，并尝试使用Path类的几种方法。

如何找类和模块的文档：问ai最高效pathlib,L文档本地查看：使用 help() 函数help(L)查看文档，print(dir(L))查看所有类和对象。

给出两个图像转换可能降低数据质量的示例。

许多旋转和缩放操作将需要插值来创建像素。这些插值像素是从原始图像数据派生的，但质量较低。

fastai 提供了哪种方法来查看DataLoaders中的数据？

‘one_batch’的方法

fastai 提供了哪种方法来帮助您调试DataBlock？

现在我们确认了正则表达式对示例的有效性，让我们用它来标记整个数据集。fastai 提供了许多类来帮助标记。对于使用正则表达式进行标记，我们可以使用RegexLabeller类。在这个例子中，我们使用了数据块 API，我们在第二章中看到过（实际上，我们几乎总是使用数据块 API——它比我们在第一章中看到的简单工厂方法更灵活）：

pets = DataBlock(blocks = (ImageBlock, CategoryBlock),
                get_items=get_image_files,
                splitter=RandomSplitter(seed=42),
                get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'),
                item_tfms=Resize(460),
                batch_tfms=aug_transforms(size=224, min_scale=0.75))
dls = pets.dataloaders(path/"images")