论文 Multimodal Object Detection via Probabilistic Ensembling 的阅读和代码复现过程记录

前言

目前需要研究的多模态信息融合增强感知课题其中很大的一部分就是多模态的目标检测技术，作为入门我需要阅读这篇比较全面同时具有开源代码的论文。虽然在github的issue中针对代码的效果有一系列的问题，但是阅读和部署学习他的理念和技术手段也是有收获的。

绪论部分

简单介绍了该多模态目标检测代码采用的是RGB和热成像（提供弱光下的特征）进行融合，其中提到proben是一种简单的非学习算法，其是用贝叶斯规则和第一原理推导出来的。

贝叶斯规则

通俗易懂的例子：我们在大街上看到一个长得五大三粗，有花臂，带着大金链子，穿着个大花褂子的大汉，那么我们很有可能会觉得此人非好人，避而远之。原因是该人在电视剧中典型的反派打扮，我们都非常熟悉，给出了一个非常主观的判断。然后过了一会，你看到了大汉去扶了老奶奶过马路，此时我们又会觉得此人是好人的概率非常大，这是为什么？

我们用数学的思维想象一下这两个问题：

• 第一步：最开始我们的判断都是根据我们以往的经验作为依据进行的主观判断，我们可以给出一个老土的叫法，称为先验判断；

• 第二步：然后我们从他们的言行中获取到了对他们的一些新的认识，我们可以将所获取到的他们的言行当做是一些新的数据；

• 第三步：我们根据获得的新数据，对之前的先验判断进行一个修正，得到一个新的判断，我们依旧给它取一个老土的名字，就叫后验判断。

• 第三步：我们根据获得的新数据，对之前的先验判断进行一个修正，得到一个新的判断，我们依旧给它取一个老土的名字，就叫后验判断。

聊到这里，我们可以做一个小总结：我们通过新获取的数据来修正我们作出的先验判断，最后得到我们新的后验判断，这就是贝叶斯的基本原理。

核心贝叶斯公式：

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)} \tag{1}$$

公式推导：

贝叶斯公式推导

1. 条件概率定义

$$P(A|B) = \frac{P(A \cap B)}{P(B)} \quad (P(B) > 0) \tag{1.1}$$ $$P(B|A) = \frac{P(A \cap B)}{P(A)} \quad (P(A) > 0) \tag{1.2}$$

2. 联合概率关系

由公式 (1.2) 得：

$$P(A \cap B) = P(B|A) \cdot P(A) \tag{1.3}$$

3. 代入条件概率公式

将公式 (1.3) 代入公式 (1.1)：

$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \tag{1.4}$$

后验概率（posterior probability）：$ P(A|B) $

似然值（likelihood）：$ P(B∣A) $

先验概率（prior probability）：$ P(A) $

4. 全概率公式展开分母

$$P(B) = \sum_{i} P(B|A_i) \cdot P(A_i) \quad \text{(全概率公式)} \tag{1.5}$$

其中 $A_i$ 是样本空间的完备事件组

5. 最终贝叶斯公式

$$\boxed{P(A|B) = \frac{P(B|A) \cdot P(A)}{\sum_{i} P(B|A_i) \cdot P(A_i)}} \tag{1.6}$$

简化版（当 $A$ 和 $A^c$ 构成完备事件组时）

$$\boxed{P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B|A) \cdot P(A) + P(B|A^c) \cdot P(A^c)}} \tag{1.7}$$

第一原则

第一性原理假设了多模态之间的条件独立性。在 ProbEn（概率集成）方法的上下文中，”first principles”（第一性原理）指的是构建该方法所依赖的最基本、最底层的概率论公理和定义，而非基于现有模型或经验的推导。具体来说，这些第一性原理包括：

1. 概率论基本公理

$$\begin{array}{c} \text{(a) 非负性:} & P(E) \geq 0 \\ \text{(b) 规范性:} & P(\Omega) = 1 \\ \text{(c) 可列可加性:} & P\left(\bigcup_{i=1}^{\infty} E_i\right) = \sum_{i=1}^{\infty} P(E_i) \quad \text{(互斥事件)} \end{array}$$

2. 条件概率定义

$$P(A|B) = \frac{P(A \cap B)}{P(B)} \quad \text{当 } P(B) > 0$$

3. 独立性公理

$$\text{事件 } A \text{ 和 } B \text{ 独立} \iff P(A \cap B) = P(A) \cdot P(B)$$

4. 条件独立性假设 (ProbEn 核心原理)

对于模态观测 $ M_1, M_2 $ 和目标状态 $ S $:

$$P(M_1, M_2 | S) = P(M_1 | S) \cdot P(M_2 | S)$$

5. 全概率公式

$$P(B) = \sum_{i} P(B | A_i) \cdot P(A_i)$$

介绍

列举了简单检测堆叠会出现多目标检测结果堆叠的问题，提出了NMS（非最大值抑制）的解决方案。

NMS非最大值抑制

简单来说就是抑制不是极大值的元素，目标检测与图像分类不同，图像分类往往只有一个输出，但目标检测的输出个数却是未知的。除了Ground-Truth（标注数据）训练，模型永远无法百分百确信自己要在一张图上预测多少物体。

NMS伪代码：

虽然有点反直觉但是情况确实如上述所说，nms的比对算法是这样进行的，选择一个元素与左右相邻的两个元素进行比较，如果他比相邻的元素都大那麽将会直接输出为maximumAt(i)。
如果出现I[i]<=I[i+1]的情况函数会直接跳转到相邻的I[i+1]将其更新为新的I[i]进行下一步比对。
在本文中将NMS也作为一种多模态融合地策略，非极大值抑制（NMS）未能融合来自低置信度模态的线索。

IoU（交并比）：

还使用了一个重叠检测平均值作为对比(检测框因该是NMS得来的)

总结：所有的一般融合方式都是1+1＜1的效果他们大多都是降低了检测的分数。而proben就是要实现1+1＞2的效果。

Multimodal Data.

• 缺乏多模态配对数据数据

• 对准RGB和热成像需要专业设备（如果后期考虑多模融合可以优先考虑RGB和深度图像结合）

许多未对齐数据集和仅仅标注了一种模态的的数据集使多模态学习变得复杂。

本文中提到了KAIST行人检测数据集其中就涉及了热成像和RGB。

Multimodal Fusion.

• 早期融合：早期融合构建了一个四通道RGB加热输入，然后由（典型的）深度网络处理。

• 中期融合：midfusion将RGB和热输入保持在不同的流中，然后在网络中合并它们的下游特征。

• 晚期融合和中期融合对比：

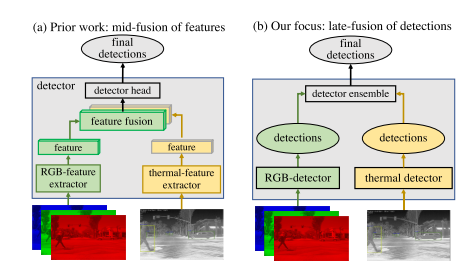
本文的工作更多的是从不同检测器的检测结果进行融合而非不同检测输入的特征。所以他在使用过程中也需要注意处理某个1探测器失效时的失踪问题。

Multimodal Object Detection via Probabilistic Ensembling

算法 1

我们假设有一个带有标签 $y$（例如，”人”）的对象，并从两种模态测量信号：$x_1$（RGB）和 $x_2$（热成像）。我们写出适用于两种模态的公式，但扩展到多种模态（在我们的实验中进行了评估）是直接的。至关重要的是，我们假设测量在给定对象标签 $y$ 的条件下是条件独立的：

$$p(x_1, x_2 | y) = p(x_1 | y) p(x_2 | y) \tag{2.1}$$

这也可以写成 $p(x_1 | y) = p(x_1 | x_2, y)$，这可能更容易直观理解。给定人员标签 $y$，预测其 RGB 外观 $x_1$；如果此预测不会改变对热信号 $x_2$ 的已有知识，则条件独立性成立。我们希望根据多模态测量推断标签：

$$p(y | x_1, x_2) = \frac{p(x_1, x_2 | y) p(y)}{p(x_1, x_2)} \propto p(x_1, x_2 | y) p(y) \tag{2.2}$$

通过将条件独立性假设从公式 (2.1) 应用到公式 (2.2)，我们得到：

$$p(y | x_1, x_2) \propto p(x_1 | y) p(x_2 | y) p(y) \propto \frac{p(x_1 | y) p(y) p(x_2 | y) p(y)}{p(y)} \tag{2.3}$$ $$\propto \frac{p(y | x_1) p(y | x_2)}{p(y)} \tag{2.4}$$

以上建议了一种简单的融合方法，当单模态特征在给定真实对象标签的条件下是条件独立的时，该方法是可证明的最优的：

1. 训练独立的单模态分类器，以预测给定每个单独特征模态的标签 $y$ 的分布 $p(y | x_1)$ 和 $p(y | x_2)$。
2. 通过将两个分布相乘、除以类别先验分布，并将最终结果（公式 4）标准化为总和为一，来生成最终分数。

tip:此处我有一点无法理解$ p(y) $按照直接理解他是这张图片是否有人的概率，这是一个令人疑惑的参数，查找以后我发现他可能是收到训练数据中有人和无人数据比例影响的一个参数，比如训练数据中一半是有人的一半是没有人的那么其就会等于0.5.（这是我目前的猜想，现在再继续阅读下文后其对$p(y)$ 有了更加深入的介绍）

关于获取类别先验概率及 ProbEn 方法的扩展

为了获得类别先验概率 $p(y)$，我们可以简单地对每个类别的样本数量进行归一化处理。将 ProbEn（公式 4）扩展到 $M$ 种模态是简单的：

$$p(y|\{x_i\}_{i=1}^M) \propto \frac{\prod_{i=1}^M p(y|x_i)}{p(y)^{M-1}} \tag{2.5}$$

这里公式 (2.5) 详细阐述了如何将 ProbEn 方法从两种模态扩展到 $M$ 种模态的情况。其中 $p(y)$ 是类别先验概率，通过归一化每个类别的样本计数得到。分子部分是 $M$ 种模态下条件概率的乘积，分母部分则是类别先验概率的 $M-1$ 次方，这样的形式体现了多模态融合过程中对各类别先验信息的综合考量。

归一化

公式 (2.5) 中提到的归一化操作，是将每个类别的样本计数进行处理，使得所有类别的概率之和为 1，具体步骤如下：

1. 统计样本计数：对于每个类别 $y$，统计训练集中属于该类别的样本数量。
2. 计算总样本数：将所有类别的样本数量相加，得到训练集的总样本数。
3. 计算归一化因子：对于每个类别 $y$，将其样本数量除以总样本数，得到 $p(y)$。 $$p(y) = \frac{\text{类别 } y\text{ 的样本数}}{\text{总样本数}}$$

这种归一化操作确保了所有类别先验概率之和为 1，符合概率的基本性质。通过这种方式，类别先验概率 $p(y)$ 反映了训练数据中各类别的相对频率，为模型提供了关于类别分布的先验信息。

是的！上面的内容进一步详细解释了 $p(y)$ 的作用和处理方式，尤其是与 ProbEn 方法的关系。以下是对 $p(y)$ 的更详细解释：

与 ProbEn 的关系

• 在公式 $p(y = k|\{x_i\}_{i=1}^M) \propto \frac{\prod_{i=1}^M p(y = k|x_i)}{p(y = k)^{M-1}} \propto \frac{\exp(\sum_{i=1}^M s_i[k])}{p(y = k)^{M-1}}$ 中，分母 $p(y = k)^{M-1}$ 直接体现了 $p(y)$ 在计算多模态后验概率时的作用。ProbEn 方法通过对各单模态的条件概率进行处理（求积后除以 $p(y = k)^{M - 1}$），实现了对多模态数据的融合，这表明 $p(y)$ 是融合过程中的一个重要参数。

确定方式

• 基于数据集统计 ：如果训练数据集中有每个类别的样本占比，如类别 $y_1$ 占 $30\%$，类别 $y_2$ 占 $70\%$，则 $p(y_1) = 0.3$，$p(y_2) = 0.7$。
• 假设均匀分布 ：当对类别分布没有特别了解时，通常假设每个类别的先验概率相等。例如一共有 $C$ 个类别，则 $p(y_i) = \frac{1}{C}$（$i = 1,2,…,C$）。
• 领域知识 ：在一些特定领域，如医学诊断中，某些疾病的发病率是已知的，就可以用发病率作为该疾病标签的先验概率。

处理缺失模态时的作用

• 在处理缺失模态时，ProbEn 能够优雅地应对。因为它基于概率归一化的多模态后验概率 $p(y|x_1, x_2)$，这些后验概率可以直接与单模态后验概率 $p(y|x_1)$ 进行比较，无需额外复杂的处理步骤，这一过程也体现了 $p(y)$ 的重要性。

总之，这段内容对 $p(y)$ 的来源、确定方法和作用等进行了深入解释，更加明确了 $p(y)$ 在 ProbEn 方法及多模态融合中的重要地位。

logits 和 softmax函数

logits 是机器学习中的一个术语，特别是在分类问题中频繁出现。它是模型输出的原始得分，通常是一个实数值，需要经过进一步处理（如 softmax 函数）才能转换为概率。

logits 的定义

logits 可以理解为模型对输入数据属于某一类别的 “置信度” 或 “偏好度” 的一种度量。它本质上是模型的最后一层输出，尚未经过激活函数（如 softmax 或 sigmoid）转换为概率值。

数学表示

假设有一个分类模型，对于输入 $x$，模型输出一个向量 $s = [s_1, s_2, \ldots, s_n]$，其中 $s_i$ 表示输入 $x$ 属于类别 $i$ 的 logit 得分。这些得分通常是通过模型的最后一层（通常是全连接层）计算得到的。

与概率的关系

logits 得分需要通过 softmax 函数转换为概率分布。softmax 函数将 logits 向量 $s$ 转换为概率向量 $p = [p_1, p_2, \ldots, p_n]$，其中：

$$p_i = \frac{\exp(s_i)}{\sum_{j=1}^n \exp(s_j)}$$

在 ProbEn 方法中的作用

在 ProbEn 方法中，logits 是单模态模型的输出。这些 logits 被用来计算条件概率 $p(y|x_i)$，然后在多模态融合过程中进行求和和归一化处理。

示例

假设一个模型有两个输出类别，logits 得分为 $s_1 = 2.0$ 和 $s_2 = 1.0$。通过 softmax 函数计算得到的概率为：

$$p_1 = \frac{\exp(2.0)}{\exp(2.0) + \exp(1.0)} \approx 0.731$$ $$p_2 = \frac{\exp(1.0)}{\exp(2.0) + \exp(1.0)} \approx 0.269$$

这个例子展示了 logits 如何被转换为概率，从而用于模型的预测。

简单来说，logits 是模型对不同类别的原始预测得分，经过 softmax 函数处理后得到概率分布。在 ProbEn 方法中，logits 是单模态模型的输出，用于后续的多模态融合和概率计算。

关于 ProbEn 方法

我们用单模态 logit 得分 $s_i[k]$ 来表示类别 $k$ 在模态 $i$ 下的概率。为简化符号，我们忽略其对底层输入模态 $x_i$ 的依赖：$p(y = k|x_i) = \frac{\exp(s_i[k])}{\sum_j \exp(s_i[j])} \propto \exp(s_i[k])$，这里我们利用了分母中的分区函数不是类别标签 $k$ 的函数这一特性。现在我们将上述表达式代入公式 (2.5)：

$$p(y = k|\{x_i\}_{i=1}^M) \propto \frac{\prod_{i=1}^M p(y = k|x_i)}{p(y = k)^{M-1}} \propto \frac{\exp(\sum_{i=1}^M s_i[k])}{p(y = k)^{M-1}}\tag{3.1}$$

ProbEn 实际上等价于对 logit 得分求和，除以类别先验概率，然后通过 softmax 进行归一化。我们的推导（公式 3.1）表明，如果不进行除法操作，仅对 logit 得分求和可能会过度计算类别先验，且这种过度计算会随着模态数量 $M$ 的增加而增长。补充材料表明，假设类别后验概率 $p(y)$ 均匀分布可以显著改善这种情况。在实践中，我们通过实验发现，即使在类别不平衡的数据集上，假设均匀先验概率也能取得出奇的良好效果。除非另有说明，这在我们的实验中是默认设置。

缺失模态

重要的是，在处理”缺失”模态时，求和和求平均的行为有显著差异。直观上看，不同的单模态检测器通常不会对同一对象同时触发。这意味着为了输出高于置信度阈值的最终检测结果（例如，用于计算精确度 - 召回率指标），需要将融合多模态检测的分数与单模态检测的分数进行比较。ProbEn 能够优雅地处理缺失模态，因为概率归一化的多模态后验概率 $ p(y|x_1, x_2) $ 可以直接与单模态后验概率 $ p(y|x_1) $ 进行比较。

边框处理

在边框处理上也采用（公式4）的办法将用 z 表示与给定检测相关的连续边界框随机变量（通过其中心坐标、宽度和高度来参数化）。

赋予检测框随机性，这里我们采用高斯分布可以写成：

$$p(\mathbf{z}|x_1, x_2) \propto p(\mathbf{z}|x_1) p(\mathbf{z}|x_2) \propto \exp\left(-\frac{\|\mathbf{z} - \boldsymbol{\mu}_1\|^2}{2\sigma_1^2}\right) \exp\left(-\frac{\|\mathbf{z} - \boldsymbol{\mu}_2\|^2}{2\sigma_2^2}\right) \tag{4.1}$$ $$\propto \exp\left(-\frac{\|\mathbf{z} - \boldsymbol{\mu}\|^2}{2\left(\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}\right)^{-1}}\right), \quad \text{where} \quad \boldsymbol{\mu} = \frac{\boldsymbol{\mu}_1/\sigma_1^2 + \boldsymbol{\mu}_2/\sigma_2^2}{1/\sigma_1^2 + 1/\sigma_2^2} \tag{4.2}$$

然后提供了三种对边框的处理方案中设置 $\sigma_i^2$的方法 ：

• 第一种方法 “avg” 固定 $\sigma_i^2 = 1$，相当于直接对边界框坐标进行简单平均。

• 第二种方法 “s - avg” 近似 $\sigma_i^2 \approx \frac{1}{p(y = k|x_i)}$，这意味着在融合边界框坐标时，更有信心的检测结果应具有更高的权重。这比简单的平均略好。

• 第三种方法 “v - avg” 训练检测器以使用高斯负对数似然（GNLL）损失来预测回归方差/不确定性，同时还进行边界框回归损失训练。有趣的是，纳入 GNLL 不仅产生了更好的方差/不确定性估计，有助于融合，还提高了训练检测器的检测性能（详细信息见补充材料）。

逆协方差矩阵

在多元高斯分布中：

$$p(\mathbf{X} = \mathbf{x}) = \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^\top \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)$$

逆协方差矩阵 $\Sigma^{-1}$ 出现在指数项中，影响分布的形状。它衡量了数据点偏离均值时的概率密度下降速度。

高斯负对数似然（GNLL）

GNLL 是 “Gaussian Negative Log Likelihood Loss” 的缩写，即高斯负对数似然损失函数。它是一种用于回归任务中的损失函数，与普通的均方误差（MSE）损失不同，GNLL 不仅考虑预测值和真实值之间的差异，还考虑了预测的不确定性（方差）。GNLL 的形式如下：

假设真实值 $ y $ 服从均值为 $ \mu $方差为 $ \sigma^2 $ 的高斯分布，则 GNLL 的计算公式为：

$$\text{GNLL} = \frac{1}{2} \left( \frac{(y - \mu)^2}{\sigma^2} + \ln \sigma^2 \right)$$

总结

本文提出了一种简单高效的后期融合办法，将两个单检测器的结果通过贝叶斯公式融合在一起，具有很强的融合灵活性和不错的效果。我认为我还需要重点学习一下有关前期融合和后期融合的两篇文章，多了解一些融合的相关方法。之后在着手寻找通过各种传感器对自然灾害检测的论文找到检测自然灾害的相关模型，数据集以及方法尝试进行前期后期中期多方面的融合，目前看来前期融合和中期融合应该是比较难的，后期融可能比较简单，应该可以对比融合前后的准确度表现出相关的提升。