svm算法学习

目标检测svm算法

支持向量机（Support Vector Machine，SVM）是一种经典的监督学习算法，用于解决二分类和多分类问题。其核心思想是通过在特征空间中找到一个最优的超平面来进行分类，并且间隔最大。

二分类直观理解

他看起来很像我之前了解过的knn算法，假设我们有一组二维空间中的数据点，这些数据点属于两个类别，分别用不同颜色表示，比如蓝色点和红色点分布在二维平面上。我们的目标是找到一条直线（在二维情况下是直线，在高维情况下是超平面），能够把蓝色点和红色点分开。这就像在一个平面上摆放着很多蓝色和红色的小球，我们希望用一根棍子（直线）把它们隔开，而 SVM 就是帮助我们找到这根最合适的棍子。

支持向量的确定

支持向量就是那些离分类超平面最近的点。这些点对分类超平面的位置确定起到关键作用。

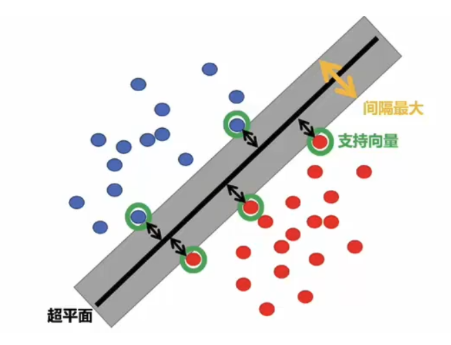
硬间隔和软间隔

硬间隔分类：在上面我们使用超平面进行分割数据的过程中，如果我们严格地让所有实例都不在最大间隔之间，并且位于正确的一边，这就是硬间隔分类。

硬间隔分类有两个问题，首先，它只在数据是线性可分离的时候才有效；其次，它对异常值非常敏感。

当有一个额外异常值的鸢尾花数据：左图的数据根本找不出硬间隔，而右图最终显示的决策边界与我们之前所看到的无异常值时的决策边界也大不相同，可能无法很好地泛化。

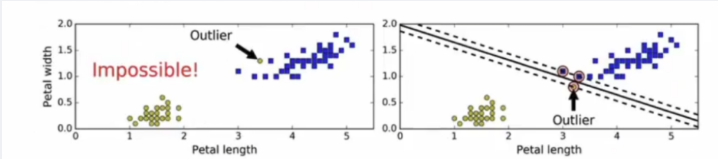
软间隔分类：要避免这些问题，最好使用更灵活的模型。目标是尽可能在保持最大间隔宽阔和限制间隔违例（即位于最大间隔之上，甚至在错误的一边的实例）之间找到良好的平衡，这就是软间隔分类。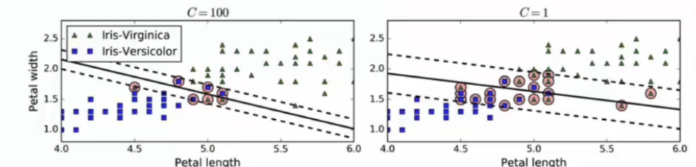

在Scikit-Learn的SVM类中，可以通过超参数C来控制这个平衡：C值越小，则间隔越宽，但是间隔违例也会越多。上图显示了在一个非线性可分离数据集上，两个软间隔SVM分类器各自的决策边界和间隔。

左边使用了高C值，分类器的错误样本（间隔违例）较少，但是间隔也较小。

右边使用了低C值，间隔大了很多，但是位于间隔上的实例也更多。看起来第二个分类器的泛化效果更好，因为大多数间隔违例实际上都位于决策边界正确的一边，所以即便是在该训练集上，它做出的错误预测也会更少。

代码演示

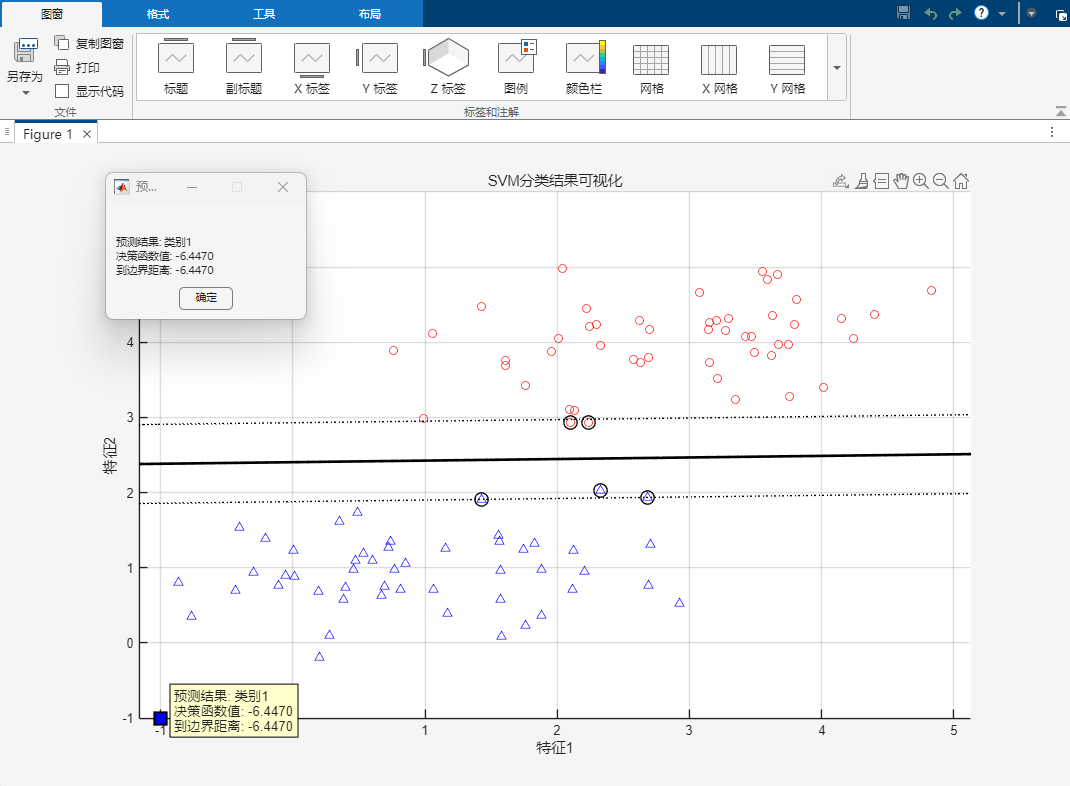
在matlab中具体运行一下svm的代码查看一下相关效果

%% 生成模拟数据（两个可线性分离的类别）
rng(1); % 固定随机种子确保可重复性
N = 50; % 每类样本数量

% 生成类别1数据（均值为[1 1]，协方差矩阵为[0.9 0.2; 0.2 0.3]）
class1 = mvnrnd([1, 1], [0.9, 0.2; 0.2, 0.3], N);

% 生成类别2数据（均值为[3 4]，协方差矩阵为[0.9 0.2; 0.2 0.3]）
class2 = mvnrnd([3, 4], [0.9, 0.2; 0.2, 0.3], N);

% 合并数据并添加标签
X = [class1; class2];          % 特征矩阵
y = [ones(N,1); -ones(N,1)];   % 标签：类别1为1，类别2为-1

%% 训练线性SVM模型
model = fitcsvm(X, y, ...
    'KernelFunction', 'linear', ... % 使用线性核
    'BoxConstraint', 1, ...        % 正则化参数
    'ClassNames', [1, -1]);         % 指定类别标签

%% 可视化结果
figure;
hold on;

% 绘制数据点
gscatter(X(:,1), X(:,2), y, 'rb', 'o^', [], 'off');
title('SVM分类结果可视化');
xlabel('特征1'); ylabel('特征2');
legend('类别1', '类别2', 'Location', 'northwest');

% 绘制决策边界
w = model.Beta;              % 获取权重向量
b = model.Bias;              % 获取偏置项
f = @(x1,x2) w(1)*x1 + w(2)*x2 + b; % 决策函数

% 创建网格用于绘制决策边界
h = fimplicit(f, [min(X(:,1))-0.5 max(X(:,1))+0.5 ...
                  min(X(:,2))-0.5 max(X(:,2))+0.5]);
h.Color = 'k';
h.LineWidth = 2;
h.LineStyle = '-';

% 绘制支持向量
sv = model.SupportVectors;
plot(sv(:,1), sv(:,2), 'ko', 'MarkerSize', 10, 'LineWidth', 1);

% 绘制间隔边界
fcontour(@(x1,x2) f(x1,x2), [min(X(:,1))-0.5 max(X(:,1))+0.5 ...
                             min(X(:,2))-0.5 max(X(:,2))+0.5], ...
         'LevelList', [-1 1], ... % 间隔边界位于f(x)=±1处
         'LineStyle', ':', ...
         'LineColor', 'k');

% 添加图例
legend('类别1', '类别2', '决策边界', '支持向量', '间隔边界');
grid on;
hold off;

%% 显示模型信息
fprintf('SVM模型参数:\n');
fprintf('权重 w = [%.4f, %.4f]\n', w(1), w(2));
fprintf('偏置 b = %.4f\n', b);
fprintf('支持向量数量: %d\n', size(sv,1));

while true
    % 提示用户输入坐标
    prompt = {'请输入特征1的值:', '请输入特征2的值:'};
    dlgtitle = 'SVM分类预测';
    dims = [1 35];
    definput = {'2', '3'}; % 默认值
    
    answer = inputdlg(prompt, dlgtitle, dims, definput);
    
    % 如果用户点击取消则退出
    if isempty(answer)
        break;
    end
    
    % 获取输入值
    x1 = str2double(answer{1});
    x2 = str2double(answer{2});
    
    % 验证输入有效性
    if isnan(x1) || isnan(x2)
        errordlg('请输入有效的数值!', '输入错误');
        continue;
    end
    
    % 预测类别
    [pred_label, score] = predict(model, [x1, x2]);
    
    % 显示结果
    if pred_label == 1
        class_name = '类别1';
        color = 'b';
    else
        class_name = '类别2';
        color = 'r';
    end
    
    % 在图上标记该点
    figure(gcf); % 回到当前图形
    hold on;
    h_point = plot(x1, x2, 's', 'MarkerSize', 12, 'LineWidth', 2, ...
                  'MarkerFaceColor', color, 'MarkerEdgeColor', 'k');
    
    % 显示信息框
    dist_to_boundary = f(x1, x2); % 计算到决策边界的函数距离
    msg = sprintf('预测结果: %s\n决策函数值: %.4f\n到边界距离: %.4f', ...
                 class_name, score(2), dist_to_boundary);
    h_text = text(x1+0.1, x2+0.1, msg, 'FontSize', 10, ...
                 'BackgroundColor', [1 1 0.8], 'EdgeColor', 'k');
    
    % 添加图例
    legend('类别1', '类别2', '决策边界', '支持向量', '间隔边界', '预测点');
    
    % 等待用户点击继续
    uiwait(msgbox(msg, '预测结果', 'modal'));
    
    % 清除临时标记
    delete(h_point);
    delete(h_text);
end

运行结果：

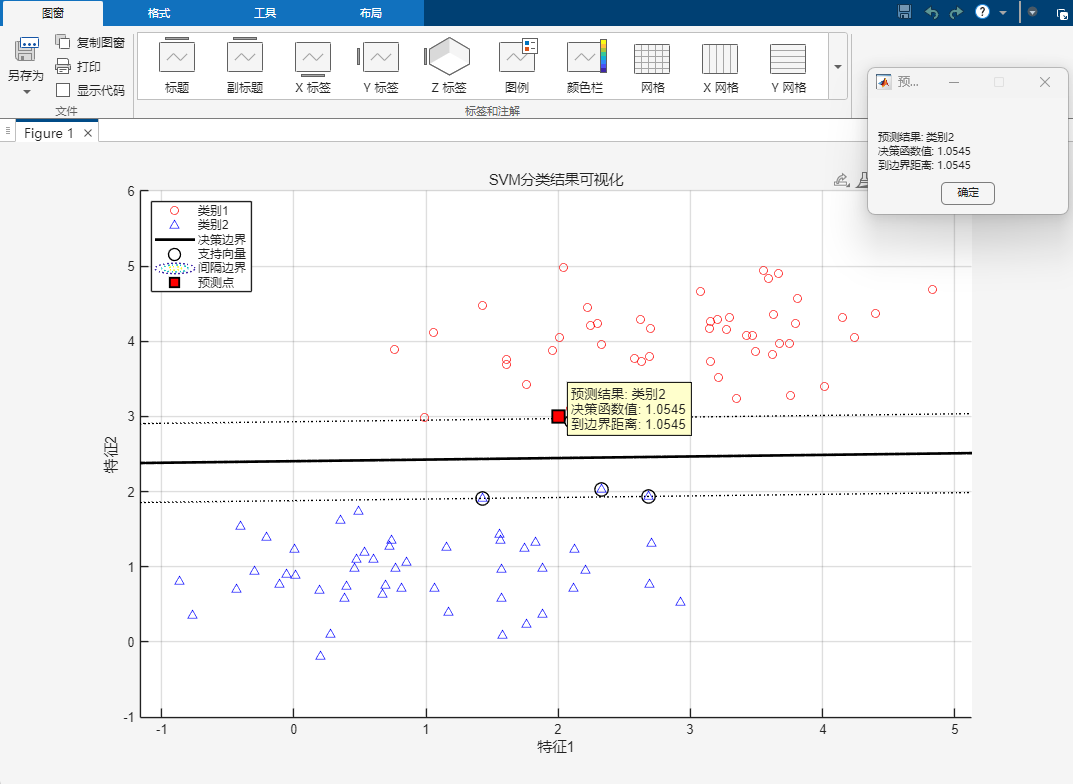
svm算法的优点和通常使用流程

1）SVM方法既可以用于分类（二/多分类），也可用于回归和异常值检测。

2）SVM具有良好的鲁棒性，对未知数据拥有很强的泛化能力，特别是在数据量较少的情况下，相较其他传统机器学习算法具有更优的性能。

• 对样本数据进行归一化

• 应用核函数对样本进行映射（最常采用和核函数是RBF和Linear，在样本线性可分时，Linear效果要比RBF好)

• 用cross-validation和grid-search对超参数进行优选

• 用最优参数调练得到模型

• 测试

算法原理

SVM通过优化一个凸二次规划问题来求解最佳的超平面，其中包括最小化模型的复杂度（即最小化权重的平方和），同时限制训练样本的误分类情况。这个优化问题可以使用拉格朗日乘子法来求解。对于非线性可分的情况，SVM可以通过核函数（Kernel Function）将输入特征映射到高维空间，使得原本线性不可分的数据在高维空间中变得线性可分。常用的核函数包括线性核、多项式核、高斯核等。

好的，以下是修改后的内容：

在支持向量机（SVM）中，分割超平面公式为：

$$w^T x + b$$

其中：

• (w^T x) ：这是向量 (w) 和向量 (x) 的点积。向量 (w) 是权重向量，它垂直于分割超平面，决定了超平面的方向。向量 (x) 是样本的特征向量。点积 (w^T x) 反映了样本点 (x) 在权重向量 (w) 方向上的投影长度。
• (b) ：它是偏置项，用于确定超平面在特征空间中的位置，相当于对超平面的平移量。通过调整 (b) 的值，可以在保持超平面方向不变的情况下，改变超平面距离原点的距离，从而影响分类边界的位置。

分割超平面的作用是将不同类别的样本分开。对于一个给定的样本 (x)，当

$$w^T x + b > 0$$

时，模型预测该样本属于正类，正类使用1表示；当

$$w^T x + b < 0$$

时，预测为负类，负类使用-1表示；而当

$$w^T x + b = 0$$

时，样本点正好位于超平面上。

分类器求解优化问题

现在我们需要做的就是找出$w$和$b$。

确定数据点到分割面的距离并确定分割面放置位置时，间隔通过$label*(w^t+b)$来计算他的函数间距（label一般取1或者-1）

注：$label*(w^t+b)×1/||x||$为点到分割面的几何距离。

找到具有最小间隔的数据点，对间隔进行最大化，写作：

$$\arg \max _ {w,b} \left\{ \min \left( \frac{\text{label} \cdot (w^T x + b)}{n}, \frac{1}{\|w\|} \right) \right\}$$

公式解释：

$\arg \max _{w,b}$ 表示我们要找到使大括号内的表达式达到最大值的 $w$ 和 $b$ 组合。而大括号内的部分是一个最小值函数 $\min (…) $，所以我们是在寻找能够使这个最小值尽可能大的 $w$ 和 $b$。

带约束条件的优化问题会让人很容易想到拉格朗日乘子法。

拉格朗日乘子法

问题定义

给定优化问题：

$$\min_{\mathbf{x}} f(\mathbf{x}) \quad \text{subject to} \quad g_i(\mathbf{x}) = 0, \ i=1,...,m$$

其中：

• $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是目标函数
• $g_i: \mathbb{R}^n \rightarrow \mathbb{R}$ 是等式约束
• $\mathbf{x} \in \mathbb{R}^n$ 是优化变量

核心原理

在约束极值点 $\mathbf{x}^*$ 处，目标函数梯度与约束函数梯度线性相关：

$$\nabla f(\mathbf{x}^*) = \sum_{i=1}^m \lambda_i \nabla g_i(\mathbf{x}^*)$$

其中 $\lambda_i$ 称为拉格朗日乘子。

拉格朗日函数

构造增广函数：

$$\mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}) = f(\mathbf{x}) + \sum_{i=1}^m \lambda_i g_i(\mathbf{x})$$

其中 $\boldsymbol{\lambda} = [\lambda_1, …, \lambda_m]^T$ 是乘子向量。

极值必要条件

极值点 $(\mathbf{x}^, \boldsymbol{\lambda}^)$ 满足：

1. 梯度条件：

   $$\nabla_{\mathbf{x}} \mathcal{L} = \nabla f(\mathbf{x}^*) + \sum_{i=1}^m \lambda_i^* \nabla g_i(\mathbf{x}^*) = \mathbf{0}$$

2. 原始可行性条件：

   $$g_i(\mathbf{x}^*) = 0, \quad \forall i=1,...,m$$

求解步骤

1. 构造拉格朗日函数 $\mathcal{L}(\mathbf{x}, \boldsymbol{\lambda})$
2. 求偏导数方程组： $$\begin{cases} \frac{\partial \mathcal{L}}{\partial x_j} = 0, & j=1,...,n \\ \frac{\partial \mathcal{L}}{\partial \lambda_i} = g_i(\mathbf{x}) = 0, & i=1,...,m \end{cases}$$
3. 解 $(n+m)$ 个方程组成的方程组
4. 验证解的极值性质（极小/极大）

不等式约束扩展 (KKT条件)

对于不等式约束 $h_j(\mathbf{x}) \leq 0$：

1. 梯度条件：

   $$\nabla f + \sum \lambda_i \nabla g_i + \sum \mu_j \nabla h_j = \mathbf{0}$$

2. 原始可行性：

   $$\begin{cases} g_i(\mathbf{x}) = 0 \\ h_j(\mathbf{x}) \leq 0 \end{cases}$$

3. 乘子非负性：

   $$\mu_j \geq 0$$

4. 互补松弛条件：

   $$\mu_j h_j(\mathbf{x}) = 0$$

关键性质

1. 梯度对齐：约束梯度张成目标梯度的正交补空间
2. 边界激活：不等式约束在 $\mu_j > 0$ 时等价于等式约束
3. 敏感性：$\lambda_i$ 表示约束 $g_i$ 变化对目标值的影响率： $$\frac{\partial f^*}{\partial c_i} = -\lambda_i$$ 其中 $g_i(\mathbf{x}) = c_i$

应用条件

1. 函数 $f$ 和 $g_i$ 连续可微
2. 约束梯度 $\nabla g_i$ 在极值点线性无关（约束规范）
3. 对于凸问题，KKT条件是充分必要条件

此框架将约束优化转化为无约束问题求解，是连续优化理论的核心工具。

公式换算

这里的约束调节都是基于数据点的，因此我们需要将超平面公式写成数据点形式：

图中的公式是对支持向量机（SVM）的优化问题进行推导后得到的形式，其推导过程涉及从原始的分类间隔最大化问题到对偶问题的转换。以下是详细的推导步骤：

原始优化问题

SVM 的原始优化目标是最大化分类间隔，同时确保所有数据点被正确分类。分类间隔的大小与 (\frac{1}{|w|}) 成正比，因此我们希望最大化 (\frac{1}{|w|})，等价于最小化 (|w|^2)。同时，约束条件是每个数据点满足 (y_i \times (w^T x_i + b) \geq 1)。

原始优化问题可以表示为：
[
\begin{align}
\min_{w, b} \quad & \frac{1}{2} |w|^2 \
\text{subject to} \quad & y_i \times (w^T x_i + b) \geq 1, \quad i = 1, 2, \ldots, N
\end{align}
]

引入拉格朗日乘子

为了求解这个带约束的优化问题，我们引入拉格朗日乘子 (\alphai \geq 0)（(i = 1, 2, \ldots, N)），构建拉格朗日函数：
[
\mathcal{L}(w, b, \alpha) = \frac{1}{2} |w|^2 - \sum{i=1}^N \alpha_i \left( y_i \times (w^T x_i + b) - 1 \right)
]

对偶问题

我们通过对拉格朗日函数进行极小化和极大化操作，将原始的约束优化问题转换为对偶问题。具体步骤如下：

1. 对 (w) 和 (b) 进行极小化：
   [
   \min_{w, b} \mathcal{L}(w, b, \alpha)
   ]

2. 对 (\alpha) 进行极大化：
   [
   \max{\alpha} \min{w, b} \mathcal{L}(w, b, \alpha)
   ]

求导并代入

通过对拉格朗日函数分别对 (w) 和 (b) 求导，并将导数等于零的条件代入，可以得到：

1. 对 (w) 求导并令导数为零：
   [
   \frac{\partial \mathcal{L}}{\partial w} = w - \sum{i=1}^N \alpha_i y_i x_i = 0 \implies w = \sum{i=1}^N \alpha_i y_i x_i
   ]

2. 对 (b) 求导并令导数为零：
   [
   \frac{\partial \mathcal{L}}{\partial b} = -\sum{i=1}^N \alpha_i y_i = 0 \implies \sum{i=1}^N \alpha_i y_i = 0
   ]

代入拉格朗日函数

将 (w = \sum{i=1}^N \alpha_i y_i x_i) 和 (\sum{i=1}^N \alpha_i y_i = 0) 代入拉格朗日函数 (\mathcal{L}(w, b, \alpha))，得到：

[
\mathcal{L} = \sum{i=1}^N \alpha_i - \frac{1}{2} \sum{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j)
]

对偶问题的优化目标

最终，对偶问题的优化目标变为：
[
\max{\alpha} \left[ \sum{i=1}^N \alphai - \frac{1}{2} \sum{i=1}^N \sum{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) \right]
]
其中，(\alpha_i \geq 0) 且 (\sum{i=1}^N \alpha_i y_i = 0)。

这个公式表示我们通过最大化这个目标函数来找到最优的拉格朗日乘子 (\alpha_i)，进而得到 (w) 和 (b)，从而确定最优分类超平面。